Consolidación 1° y 2° Evaluación

Ejercicios Pág.166 : 5, 10, 14, 20 y 21.

Ejercicios Inicio Tema 12: Geometría Espacial

Ejercicio 1: ¿De esos once cuerpos geométricos, cuáles son POLIEDROS CONVEXOS y cuáles son CUERPOS DE REVOLUCIÓN?

A)Poliedro Convexo
B)Poliedro convexo
C)Poliedro Convexo
D)Poliedro convexo
E)Poliedro Convexo
F)Cuerpo De Revolución
G)Cuerpo De Revolución
H)Poliedro Convexo
I)Cuerpo De Revolución
J)Cuerpo De Revolución
K)Cuerpo De Revolución

Ejercicio 2: Escribe una tabla para comprobar que la fórmula de Euler se verifica en diferentes poliedros convexos.

	Caras (C)	Aristas (A)	Vértices (V)	C + V = A + 2
Prisma Rectangular	4 caras	12 aristas	8 vértices	4+8= 12+2
Prisma Pentagonal	5 caras	15 aristas	10 vértices	5+10=15+2
Antiprisma Cuadrado	10 caras	16 aristas	8 vértices	10+8=16+2
Antiprisma Pentagonal	12 caras	20 aristas	10 vértices	12+10=20+2
Pirámide Triangular	4 caras	6 aristas	4 vértices	4+4=6+2
Pirámide Triangular Truncada	5 caras	9 aristas	6 vértices	5+6=9+2

Ejercicio 3: Investiga sobre la vida y obra de Arquímedes.

Arquímedes (287-212 a.C.), Se le considera padre de la ciencia mecánica y el científico y matemático más importante de la edad antigua.En el campo de las Matemáticas puras su obra más importante fue el descubrimiento de la relación entre la superficie y el volumen de una esfera y el cilindro que la circunscribe; por esta razón mandó Arquímedes que sobre su tumba figurase una esfera inscrita en un cilindro.

A él le debemos inventos como la rueda dentada y la polea para subir pesos sin esfuerzo. También a él se le ocurrió usar grandes espejos para incendiar a distancia los barcos enemigos.

En Geometría sus escritos más importantes fueron:

• De la Esfera y el Cilindro, donde introduce el concepto de concavidad,así como ciertos postulados referentes a la línea recta.
• De los Conoides y Esferoides en donde define las figuras engendradas por la rotación de distintas secciones planas de un cono.
• De las Espirales en donde analiza estas importantes curvas y analiza sus elementos más representativos.

    En Aritmética son, fundamentalmente dos los escritos más interesantes:

• El Arenario en el que expone un método para escribir números muy largos dando a cada cifra un orden diferente según que su posición.

Ejercicio 4: Publica en tu blog una entrada con los cinco poliedros regulares también llamados sólidos platónicos. ¿Por qué se llaman así? ¿Y por qué sólo hay 5? ¿De dónde reciben el nombre los sólidos arquimedianos?

Poliedros Regulares :

- Tetraedro

-Cubo

-Octaedro

-Dodecaedro

Icosaedro

Se denominan así debido a ser sus caras polígonos regulares iguales, y todos sus diedros y ángulos poliedros también iguales. 

 Un poliedro es regular si todas sus caras son polígonos regulares idénticos y si en todos sus vértices concurren el mismo número de caras. Por lo tanto, es imposible formar un poliedro con solo dos triángulos en cada vértice.

Ejercicio 5:

• ¿Qué figura plana hay que girar y alrededor de qué eje para obtener un CILINDRO?

Se obtiene al girar un rectángulo alrededor de un lado.

• ¿Qué figura plana hay que girar y alrededor de qué eje para obtener un CONO?

Se obtiene al girar un triángulo rectángulo alrededor de un vértice.

• ¿Qué figura plana hay que girar y alrededor de qué eje para obtener un ESFERA?

Se obtiene al girar un semicírculo desde su centro.


Ejercicio 4.2 : Clasifica el siguiente cuerpo geométrico cuyas caras son cuadrados y triángulos equiláteros. ¿Es un poliedro semirregular?

No, no es un poliedro semirregular. Es un sólido, el cual está formado por la suma entre un cubo y una pirámide cuadrangular regular que tiene los aristas de base coincidentes con los aristas de una cara del cubo. 




Ejercicio 7: ¿Los cuerpos de revolución son convexos?

No, no son convexos, ya que no hay ningún segmento que una dos puntos que esté contenido en dicho cuerpo de revolución.

Ejercicio 8: ¿Qué es TRUNCAR un cuerpo geométrico en el espacio? Pon cuatro ejemplos diferentes. ¿Si truncamos un cuerpo geométrico convexo se obtiene siempre otro cuerpo geométrico convexo (o mejor dicho, dos, por cada truncamiento)?

- Truncar significa cortar los vértices o los aristas de dicho cuerpo geométrico.
- Ejemplos:

1.Pirámide truncada :


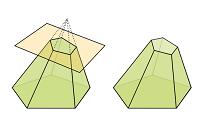
2. Cubo truncado :



3. Tetraedro truncado :



4. Cono truncado :




- No siempre, porque hay casos en los que se deshace el hecho de que sea un cuerpo geométrico al diseccionarlo o cortarlo dicho cuerpo,



Se te podría ocurrir hacer la siguiente pregunta: ¿Hay más poliedros convexos?

Solo existen 5 poliedros regulares, pero existen más polígonos convexos que no son regulares, como es, por ejemplo, la pirámide.

Clasificación de Cuadriláteros y Paralelogramos

Cuadriláteros :
 
   - Trapezoide: Es un cuadrilátero convexo el cual no tiene lados paralelos.
      *Cometa o Deltoide: Es un cuadrilátero no regular cuyos lados contiguos son iguales dos a dos.
        También es denominado como un trapezoide con dos pares de lados consecutivos iguales.
   - Trapecio: Es un cuadrilátero el cual tiene únicamente dos lados paralelos.
   - Paralelogramo: Es un cuadrilátero cuyos pares de lados opuestos son iguales y además son paralelos dos a dos.

Cuadrilátero Cóncavo: Es un cuadrilátero cuyos ángulos interiores son menores a 180 grados.

Paralelogramos :

  - Cuadrados: Es un paralelogramo cuyos cuatro lados sin iguales y sus cuatro ángulos interiores son rectos, es decir, miden todos noventa grados.
 - Rectángulo: Es un paralelogramo cuyos cuatro lados forman ángulos rectos entre sí.
 - Rombo: Es un paralelogramo cuyos cuatro lados son de la misma longitud.
 - Romboide: Es un paralelogramo cuyos lados contiguos no son iguales y dos de sus ángulos son mayores que los otros dos.

Los Centros de un Triángulo

Centros de un Triángulo :



- Baricentro :

• El baricentro, también llamado centroide o centro de gravedad, de un triángulo es el punto de intersección de dos medianas de dicho triángulo. Una mediana es el segmento que une un vértice con el punto medio del lado opuesto.
• ¡No importa qué dos medianas! Pues la tercera mediana también pasa por el baricentro.

- Circuncentro : 

• El circuncentro de un triángulo es el centro de la circunferencia inscrita al triángulo. El radio de dicha circunferencia es la distancia a cada uno de sus vértices que es la misma .
• El circuncentro es el punto de intersección de las mediatrices de dicho triángulo. Una mediatriz es la recta perpendicular a un lado que pasa por el punto medio del mismo.
• ¡No importa qué dos mediatrices! Pues la tercera mediatriz también pasa por el circuncentro.

- Incentro : 

• El incentro es el centro de la circunferencia inscrita al triángulo. El radio de dicha circunferencia es la distancia a cada uno de sus lados que es la misma .
• El incentro es el punto de intersección de las bisectrices de dos ángulos de dicho triángulo. Una bisectriz de un ángulo es la recta que divide al ángulo en dos ángulos iguales.
• ¡No importa qué dos bisectrices! Pues la tercera bisectriz también pasa por el incentro.

- Ortocentro : 

• El ortocentro de un triángulo es el punto de intersección de las dos alturas de dicho triángulo. Una altura es el segmento que parte de un vértice y es perpendicular al lado opuesto a dicho vértice.
• ¡No importa qué dos alturas! Pues la tercera altura también pasa por el ortocentro.

- La recta de Euler : El baricentro, el circuncentro y el ortocentro de cualquier triángulo ESTÁN ALINEADOS. Dicha recta se llama recta de Euler.

Ángulos de una Circunferencia

Ángulo Central : Aquel que tiene su vértice en el centro.

Ángulo Interior : Aquel que tiene su vértice en un punto interior del círculo.

Ángulo Inscrito : Aquel que tiene su vértice en un punto de la circunferencia.

Ángulo Exterior : Aquel que tiene su vértice en un punto exterior de la circunferencia.

Ángulos de un Polígono

Ángulo Central : Aquel cuyos lados son dos radios consecutivos del polígono.

Ángulo Exterior: Aquel que es formado por un lado de un polígono y la prolongación del lado adyacente.

Ángulo Interior: Aquel formado por dos lados de un polígono que comparten un vértice común dentro de un polígono.